当下信息技术的高速发展促进了通信主体逐渐从人类个体发展为万物互联。在新一代工业现场网络中,海量的分布式网络信息需要被及时和可靠地转发和传输,对实时性、确定性和传输抖动具有严格要求。为此,IEEE 802.1 TSN工作组在现有以太网协议的基础上扩展了带宽预留、流量整形、时钟同步等一系列标准,构建覆盖上述需求的时间敏感网络(Time-Sensitive Networking, TSN)。
一、研究动机
近年来,TSN的调度方法研究层出不穷,从围绕最优性求解和调度分析的SMT[1]和ILP[2]问题构建逐渐演变为考虑增量调度[3]-[4]、分组调度[5]-[6]和其他启发式调度方法[7]的优化调度问题,以降低TSN的调度复杂度,减少调度算法运行时间,提高调度方案部署效率。在优化调度过程中,对TSN机制特性的分析和应用是确保优化策略有效/高效与否的核心因素。现有的调度和优化策略主要基于数据流间的直观联系和数据流集的数理统计结果,此类弱解释性的优化策略可能会造成未知的甚至不可靠的调度设计。基于此,本工作旨在对TSN调度机制中的流冲突和流依赖关系进行机理性分析,并据此设计一种高效调度算法,以降低调度复杂度;同时考虑网络链路的负载均衡性,以优化非周期性和周期性流量混合网络中的流量突发问题。
二、问题描述
本工作以TSN标准IEEE 802.1 Qch中的CQF(Cyclic Queuing and Forwarding)模型为配置基准,通过设计周期性时间敏感流量的网络注入时间调节流量的时隙偏移,以达成网络流量间的时隙交错,从而避免冲突发生。针对CQF模型中乒乓队列周期性循环交替的出入队配置机制,其基于流量注入时间设计的调度问题建模如下:
1. 截止时间约束
CQF模型中乒乓队列的配置和传输方式,使得数据流在网络中的传输时间限制在
其中为传输时隙长度,
为数据流
的路由跳数。注入时间
的引入增加了其网络传输时延,同时需要满足其流量截止时间
的要求,即:
2. 时隙容量约束
通过设计时间偏移和时隙长度
,网络中有限的时隙和队列资源试图被合理分配给每个数据流,以避免时隙溢出的发生,该考量通过以下约束表征:
其中,通过模操作判定某个目标数据流
对目标时隙
的占用情况;
考虑时隙长度和队列长度的下界表征时隙容量。
3. 网络负载均衡目标
本工作考虑了实际工业场景中周期性/非周期性流量共存的问题,通过优化周期性流量调度的时隙负载均衡性,以保证时间敏感的非周期性流量的QoS要求,即:
三、机制分析
本工作通过对周期性流量的序列化表述,对TSN调度问题的流量冲突和流量依赖关系进行了分析,得到了反映流间依赖关系的调度灵活性指标和描述流间冲突关系的等价判定条件。
1. 流量序列化表述
对于CQF模型,每当数据流到达某个节点
时,其当前传输时延可以被认为是恒定的,即其在相应链路
上的转发时间保持周期性。本工作将符合上述特性的数据流序列化表征为
2. 调度灵活性指标
TSN调度过程可以看做目标数据流在其链路传输时间线上的位置选择,不同的位置占用模式呈现出不同的调度和传输结果。下图表现了当数据流的注入时间变化时,链路上数据流构成的位置占用模式也会发生变化。然而,由于TSN门控列表和数据流的周期性特性,位置占用模式的数量是有限的,它们构成了该链路上的可行调度空间, 其大小反映了调度灵活性。
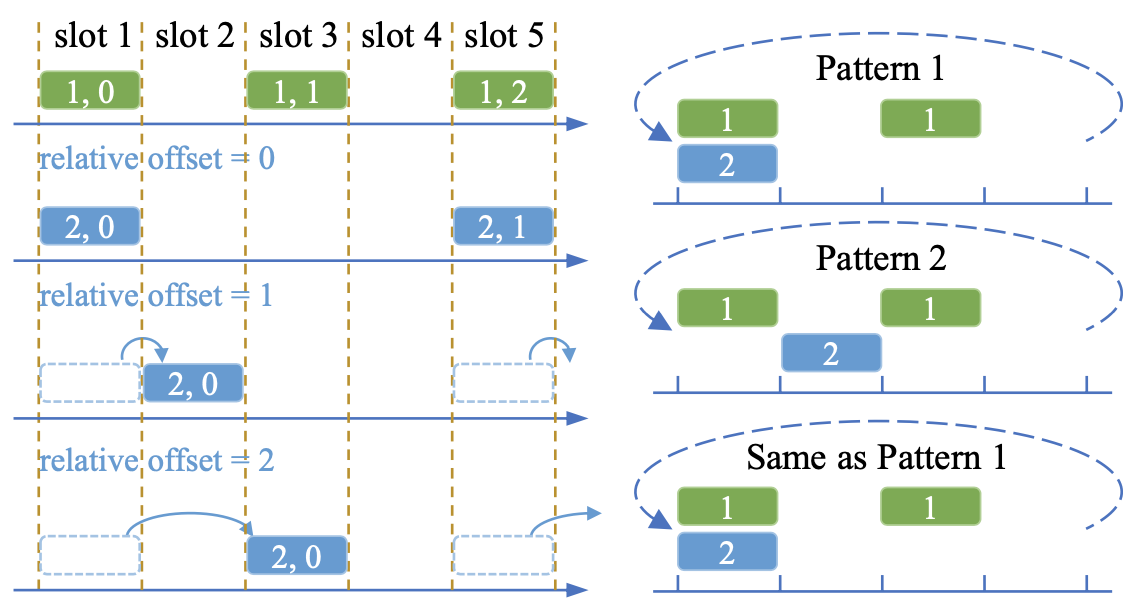
图1 位置占用模式
本工作基于整数和同余理论,对该指标进行了解析和描述,最终得到了对于链路上的n个数据流序列,其调度灵活性表述为
3. 时隙占用等价判定条件
TSN调度问题的核心在于流量间的冲突避免,不同流量对于同一时隙的占用判定是其中的关键一环。目前普遍的判定方式需要逐时隙/逐数据帧进行,这种方法虽然有效,但是牺牲了一定的可扩展性,本工作给出了一个逐流的时隙占用判定定理,其结论与上述方法等价,但具备更优的判定效率和可扩展性。
定理一:对于n个流序列,以下两个命题等价:
命题1:对于任意的流序列对和
,满足
;
命题2:存在时隙满足
,即它们存在共同的时隙占用。
四、算法设计
根据调度灵活性分析,CQF调度问题的可行空间为。对于第二部分的优化问题,本工作将其转化为MIQCP问题并利用Gurobi进行了求解,发现其为指数复杂度的NP-hard问题。为此,本工作给出了一种并行架构下的增量调度方法,其中,将不同的时隙长度
分配给独立的计算单元以实现并行计算;对每一个
下的流量注入时间设计采用增量式的贪婪调度方法,该方法首先通过本工作给出的基于调度灵活性的排序指标进行流量排序,在每一次增量调度过程中,被调度数据流
的注入时间选择被限制在本工作给出的可变搜索边界中,以剔除无效的搜索空间;最后,给出一种基于定理一的时隙占用量判定方法,其首先通过命题1进行流量间关系判定,而后依次构建冲突图,并将最大占用时隙的查找问题转化为最大权团问题,本工作同样给出了该问题的求解方法,从而实现CQF模型下的数据流高效调度。
本工作所述的增量调度算法和时隙占用量判定算法如下所示:

并行增量调度器

时隙占用判定算法
其中,基于调度灵活性的排序指标表述为
数据流的可变搜索边界表述为
五、性能评估和验证
本工作从调度效率、可扩展性以及性能调优等角度对所提算法进行了评估和验证。如图2所示,相较于现用的调度方法,我们的算法(FLJ-VB)运算效率在复杂流属性环境中提升了至少1500倍,同时,其负载均衡能力也得到了约1%的优化,这提升了调度问题的可扩展性;图3在图一算法的基础(流量随机排序)上,通过调度灵活性的流量降序排序(PDV Descend)进一步提升了约8倍的调度效率,或通过反之的流量升序排序(PDV Ascend)可以进一步优化可扩展性;图4则评估了各并行单元不同时隙长度下的负载均衡性与传输实时性的trade-off问题,这有助于在实际场景的调度过程中更具偏好的性能调优。

图2 调度算法性能比照
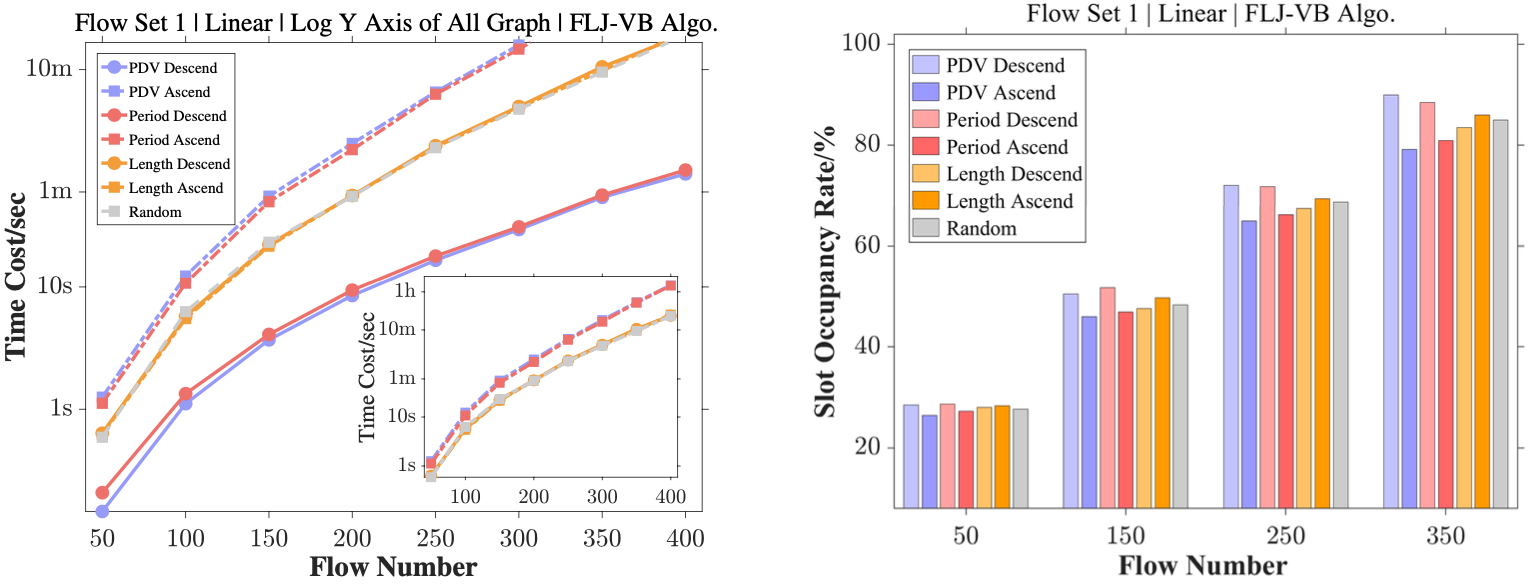
图3 排序策略性能比照
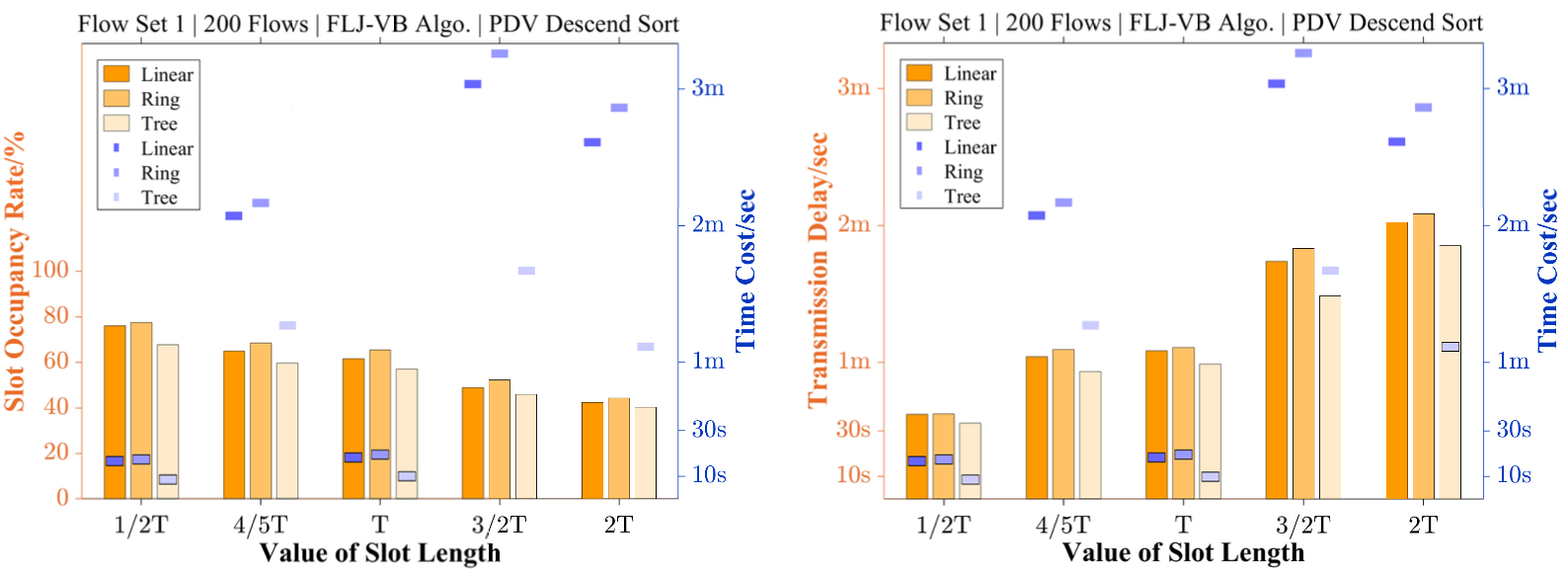
图4 各并行单元性能比照
六、总结与未来工作
该工作中旨在研究TSN机制的机理性分析和优化调度,提出了一种基于整数理论的流序列分析方法,并推导出了调度灵活度指标和一种高效的时隙占用判定定理。基于此,该工作以CQF模型为配置实施例,设计了一种高效的时间敏感流量调度算法,从而降低了调度问题的时间复杂度,同时增强了网络的负载均衡性。考虑到该方法刚刚被提出,其更深层次的调度优化能力还待挖掘。
参考文献:
[1] N. Reusch, "Window-Based Schedule Synthesis for Industrial IEEE 802.1Qbv TSN Networks," WFCS, 2020.
[2] P. Pop, "Design optimisation of cyber-physical distributed systems using IEEE time-sensitive networks," IET Cyber-Phys. Syst. Theory Appl., 2016.
[3] W. Quan, "On-line Traffic Scheduling optimization in IEEE 802.1Qch based Time-Sensitive Networks," HPCC/SmartCity/DSS, 2020.
[4] N. G. Nayak, "Incremental Flow Scheduling and Routing in Time-Sensitive Software-Defined Networks," IEEE Trans. Ind. Informat., 2018.
[5] R. Mahfouzi, "Stability-aware integrated routing and scheduling for control applications in Ethernet networks," DATE, 2018.
[6] A. A. Atallah, "Routing and Scheduling of Time-Triggered Traffic in Time-Sensitive Networks," IEEE Trans. Ind. Informat., 2020.
[7] J. Yan, "Injection Time Planning: Making CQF Practical in Time-Sensitive Networking," INFOCOM, 2020.
本研究刊发于:
Y. Zhang, Q. Xu, L. Xu, C. Chen and X. Guan, "Efficient Flow Scheduling for Industrial Time-Sensitive Networking: A Divisibility Theory Based Method," in IEEE Transactions on Industrial Informatics, doi: 10.1109/TII.2022.3151810.
本文已发布于微信公众号“确定性网络系统技术”,全文链接:https://mp.weixin.qq.com/s/kRqjOimj_MU-ym0hc8mYqQ